emporiumlooki.blogg.se - Scatter plot

SCATTER PLOT CODE

Some customers want cheaper cell phones even if they don’t have great performance. Customers prefer getting lower-price but good-performance cell phones, while fewer customers are looking for high-end and high-priced cell phones. Cluster 1 in blue color has more outliers as compared with cluster 3. (low price, high rating) in orange color is most dense and tightly packed.

A few outliers are indicating larger area houses available for lower prices.įigure 6 shows three different color-coded clusters giving us an immediate idea that cluster 2.

It is like logarithmic, power, polynomial, etc.

We can try different trend line models provided by Tableau.

It has a p-value less than 0.0001 and R-squared 0.33, indicating that this might not be the best model.

We have drawn a linear trend line in which both variables that transforms by the natural logarithm ln(Y), ln(X) before the model is estimate.

Here, we can see from Figure 2 that data points are concentrate in the lower price and lower area range.

So, We will plot a scatter plot of two measures – area against price and the trend lines for both. As a general rule, a low p-value usually less than 0.005 and an R-squared value closer to 1 signifies a good model.įor instance, let us look at a use case with a data set containing different dimensions like furnishing – furnished or unfurnished, locality, status – ready to move or almost ready, transaction – New or resale, type – apartment or builder floor (entire floor for the occupant), per square feet price and price. They give us the p-value and R-squared values, which tell us how well our line is fitting to the data. They indicate how strong or weak the relationship is and if any outliers are affecting the trend line. Such that it is the best fit for the data. A trend line is an equation that shows the relationship between measures.

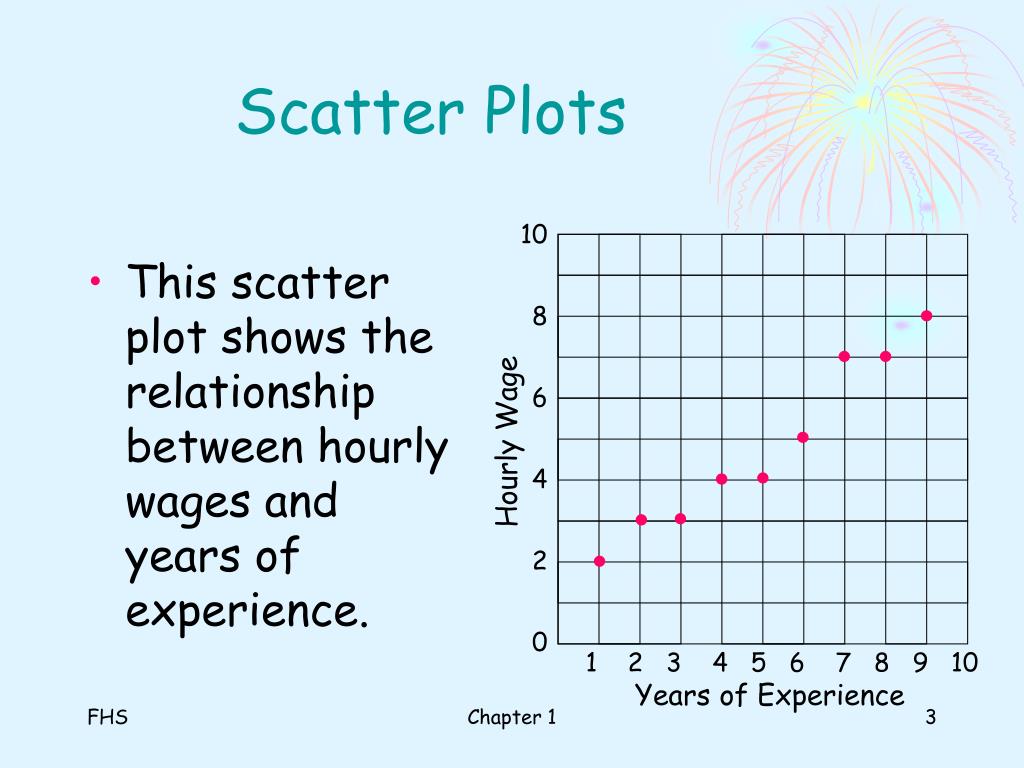
The line passing through the points is naming a trend line which shows the correlation of variables. Negative: As x co-ordinate increases, y co-ordinate decreases. Jira Certification Course for Business analyst.

BA Training with Investment Banking Domain.

You can assign different colors or markers to the levels of these variables. You can use categorical or nominal variables to customize a scatter plot. Either way, you are simply naming the different groups of data.

SCATTER PLOT CODE

You can use the country abbreviation, or you can use numbers to code the country name. Country of residence is an example of a nominal variable. For example, in a survey where you are asked to give your opinion on a scale from “Strongly Disagree” to “Strongly Agree,” your responses are categorical.įor nominal data, the sample is also divided into groups but there is no particular order. With categorical data, the sample is divided into groups and the responses might have a defined order. Scatter plots are not a good option for categorical or nominal data, since these data are measured on a scale with specific values. Some examples of continuous data are:Ĭategorical or nominal data: use bar charts Scatter plots make sense for continuous data since these data are measured on a scale with many possible values. Scatter plots and types of data Continuous data: appropriate for scatter plots

Annotations explaining the colors and markers could further enhance the matrix.įor your data, you can use a scatter plot matrix to explore many variables at the same time. The colors reveal that all these points are from cars made in the US, while the markers reveal that the cars are either sporty, medium, or large. There are several points outside the ellipse at the right side of the scatter plot. From the density ellipse for the Displacement by Horsepower scatter plot, the reason for the possible outliers appear in the histogram for Displacement. In the Displacement by Horsepower plot, this point is highlighted in the middle of the density ellipse.īy deselecting the point, all points will appear with the same brightness, as shown in Figure 17. This point is also an outlier in some of the other scatter plots but not all of them. In Figure 16, the single blue circle that is an outlier in the Weight by Turning Circle scatter plot has been selected. It's possible to explore the points outside the circles to see if they are multivariate outliers. The red circles contain about 95% of the data. The scatter plot matrix in Figure 16 shows density ellipses in each individual scatter plot.